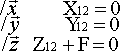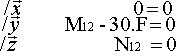RESOLUTION D'UN PROBLEME DE STATIQUE ANALYTIQUE :

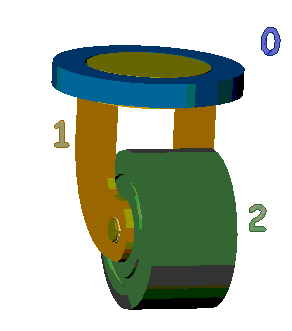
On prendra le support d'une roue orientable de chariot :

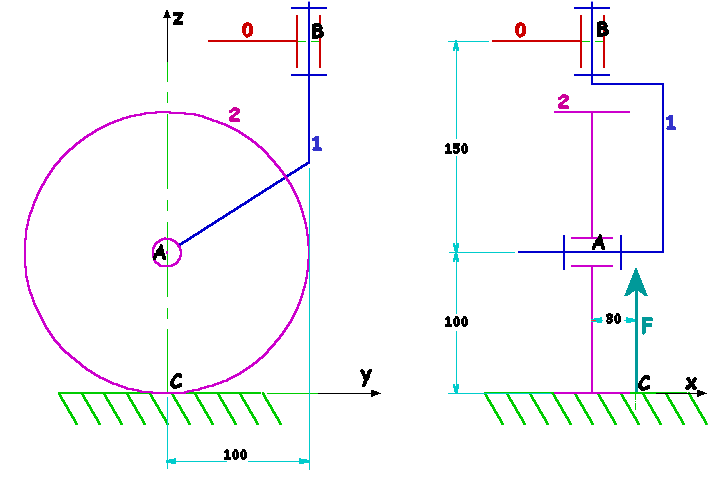
La roue (2) d'un chariot, est guidée en rotation par rapport au solide (1) autour de l'axe par l'intermédiaire de l'axe (3) et de 2 roulements à billes. De plus la pièce (1) est elle guidée en rotation par rapport au bâti (0) suivant l'axe . On modélise en outre l'action du sol sur la roue (2) par une force de sens et de norme 300 daN, appliquée en C.

Partie 1 : on isole la roue (2)

Etape 1 : Bilan des actions mécaniques extérieures :
Le bilan des actions mécaniques extérieures permet de faire apparaître toutes les inconnues du problème (actions mécaniques ou actions transmissibles dans les liaisons).
Pour cela, on écrit sous forme de torseurs, les actions mécaniques appliquées au solide isolé. Ceux sont, soit des actions mécaniques (forces, moments, action de pesanteur ...), soit des actions transmissibles dans les liaisons (on écrit alors le torseur d'action transmissible dans la liaison considérée).

Pour la roue (2), on a :
- L'action du sol sur la roue, c'est un glisseur (une force) appliqué en C, on le notera :
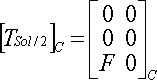                                                   F = 300 daN (voir hypothèses)
- L'action dans la liaison pivot d'axe (A, x) entre (2) et (1) :

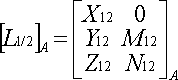
On a ici 5 inconnues, que l'on appelle inconnues de liaison.

Remarque : Les torseurs s'écrivent au point d'application de l'action mécanique, pour ce qui est des torseurs d'actions transmissibles dans les liaisons, on précisera les caractéristiques de la liaison (centre, axe ou normale)


Étape 2 : Transport des torseurs au même point de réduction
Afin de pouvoir appliqué le PFS, on a besoin d'exprimer tous les torseurs au même point (addition). On les transportera donc, au moyen de la relation des champs des moments.
Le choix du point de transport est soit imposé par le texte du problème, soit à choisir de manière à réduire le nombre de calculs.
Transport du torseur :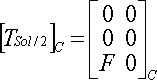

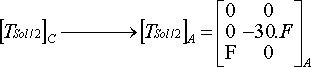Étape 3 : Application du PFS
On applique ici, le PFS tel qu'il est énoncé :
Le solide (2) est en équilibre si et seulement si :
           

Étape 4 : Écriture des équations
Les équations découlent du PFS par l'écriture développée du théorème de la résultante et du théorème des moments :

Étape 5 : Résolution totale ou partielle des équations :

Si on le peut, on résout totalement de manière à faire apparaître toutes les inconnues, ou partiellement pour faire apparaître des relations entre les inconnues du problème.
On obtient :

Étape 6 : Écriture des résultats
On écrit enfin, les torseurs du Bilan des actions mécaniques extérieures, en remplaçant les inconnues par les valeurs trouvées :




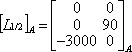
Application :
Partie 2 : Isolement du solide 1
Appliquer le PFS